This module contains all basis function routines. More...
Go to the source code of this file.
Data Types | |
| interface | basis_routines::basis_evaluate_xi |
| Evaluates the appropriate partial derivative index for the specificied basis function at a Xi location. More... | |
| interface | basis_routines::basis_gauss_points_calculate |
| Evaluates the list of gauss points and weights for a given basis type and order. More... | |
| interface | basis_routines::basis_interpolate_gauss |
| Interpolates the appropriate partial derivative index of the elements parameters for basis function at a Gauss point. More... | |
| interface | basis_routines::basis_interpolate_xi |
| Interpolates the appropriate partial derivative index of the elements parameters for basis function at Xi location. More... | |
| interface | basis_routines::basis_interpolate_local_face_gauss |
| Interpolates the requested partial derivative index(ices) of the element parameters for basis function at a face Gauss point. More... | |
| interface | basis_routines::basis_interpolation_xi_set |
| Sets/changes the interpolation type in each Xi direction for a basis. More... | |
| interface | basis_routines::basis_number_of_xi_set |
| Sets/changes the number of Xi directions for a basis. More... | |
| interface | basis_routines::basis_type_set |
| Sets/changes the type for a basis. More... | |
| interface | basis_routines::basis_collapsed_xi_set |
| Sets/changes the collapsed Xi flags for a basis. More... | |
| interface | basis_routines::basis_quadrature_order_set |
| Sets/changes the order of a quadrature for a basis quadrature. More... | |
| interface | basis_routines::basis_quadrature_type_set |
| Sets/changes the quadrature type for a basis. More... | |
| interface | basis_routines::simplex_linear_evaluate |
| interface | basis_routines::simplex_quadratic_evaluate |
| interface | basis_routines::simplex_cubic_evaluate |
| interface | basis_routines::basis_lhtp_basis_evaluate |
| Evaluates the Lagrange/Hermite/Fourier tensor product basis function for the given basis. More... | |
Modules | |
| module | basis_routines |
| This module contains all basis function routines. | |
Functions/Subroutines | |
| subroutine, public | basis_routines::bases_finalise (ERR, ERROR,) |
| Finalises the bases and deallocates all memory. More... | |
| subroutine, public | basis_routines::bases_initialise (ERR, ERROR,) |
| Initialises the bases. More... | |
| subroutine, public | basis_routines::basis_create_finish (BASIS, ERR, ERROR,) |
| Finishes the creation of a new basis. More... | |
| subroutine, public | basis_routines::basis_create_start (USER_NUMBER, BASIS, ERR, ERROR,) |
| Starts the creation of a new basis The default values of the BASIS attributes are: More... | |
| recursive subroutine | basis_routines::basis_destroy_number (USER_NUMBER, ERR, ERROR,) |
| Destroys a basis identified by its basis user number. More... | |
| recursive subroutine, public | basis_routines::basis_destroy (BASIS, ERR, ERROR,) |
| Destroys a basis. More... | |
| real(dp) function | basis_routines::basis_evaluate_xi_dp (BASIS, ELEMENT_PARAMETER_INDEX, PARTIAL_DERIV_INDEX, XI, ERR, ERROR) |
| Evaluates the appropriate partial derivative index at position XI for the basis for double precision arguments. Note for simplex basis functions the XI coordinates should exclude the last area coordinate. More... | |
| subroutine | basis_routines::basis_gauss_points_calculate_dp (basis, order, numCoords, numberGaussPoints, gaussPoints, gaussWeights, err, error,) |
| Calculates the gauss points and weights for a basis function of a particular order. More... | |
| recursive subroutine | basis_routines::basis_family_destroy (USER_NUMBER, FAMILY_NUMBER, ERR, ERROR,) |
| Destroys a basis identified by its basis user number and family number. Called from the library visible routine BASIS_DESTROY. More... | |
| recursive subroutine | basis_routines::basis_family_number_find (USER_NUMBER, FAMILY_NUMBER, BASIS, ERR, ERROR,) |
| Finds and returns in BASIS a pointer to the basis with the given USER_NUMBER and FAMILY_NUMBER. If no basis with that number and family number exists then BASIS is returned nullified. More... | |
| subroutine | basis_routines::basis_finalise (BASIS, ERR, ERROR,) |
| Finalises a basis and deallocates all memory. More... | |
| subroutine | basis_routines::basis_initialise (BASIS, ERR, ERROR,) |
| Initialises a basis. More... | |
| real(dp) function | basis_routines::basis_interpolate_gauss_dp (BASIS, PARTIAL_DERIV_INDEX, QUADRATURE_SCHEME, GAUSS_POINT_NUMBER, ELEMENT_PARAMETERS, ERR, ERROR) |
| Interpolates the appropriate partial derivative index of the element parameters at a gauss point for the basis for double precision arguments. Note the interpolated value returned needs to be adjusted for the particular >coordinate system with COORDINATE_INTERPOLATE_ADJUST. More... | |
| real(dp) function | basis_routines::basis_interpolate_local_face_gauss_dp (BASIS, PARTIAL_DERIV_INDEX, QUADRATURE_SCHEME, LOCAL_FACE_NUMBER, GAUSS_POINT_NUMBER, FACE_PARAMETERS, ERR, ERROR) |
| Interpolates the appropriate partial derivative index of the element local face parameters at a face gauss point for the basis for double precision arguments. Note the interpolated value returned needs to be adjusted for the particular >coordinate system with COORDINATE_INTERPOLATE_ADJUST. More... | |
| real(dp) function | basis_routines::basis_interpolate_xi_dp (BASIS, PARTIAL_DERIV_INDEX, XI, ELEMENT_PARAMETERS, ERR, ERROR) |
| Interpolates the appropriate partial derivative index of the element parameters at position XI for the basis for double precision arguments. Note the interpolated value returned needs to be adjusted for the particular coordinate system with COORDINATE_INTERPOLATE_ADJUST. Note for simplex basis functions the XI coordinates should exclude the last area coordinate. More... | |
| subroutine, public | basis_routines::basis_interpolation_xi_get (BASIS, INTERPOLATION_XI, ERR, ERROR,) |
| Gets/changes the interpolation type in each xi directions for a basis identified by a pointer. More... | |
| subroutine | basis_routines::basis_interpolation_xi_set_number (USER_NUMBER, INTERPOLATION_XI, ERR, ERROR,) |
| Sets/changes the interpolation type in each xi directions where the basis is identified by user number. More... | |
| subroutine | basis_routines::basis_interpolation_xi_set_ptr (BASIS, INTERPOLATION_XI, ERR, ERROR,) |
| Sets/changes the interpolation type in each xi directions for a basis identified by a pointer. More... | |
| subroutine | basis_routines::basis_lhtpbasiscreate (basis, err, error,) |
| Creates and initialises a Lagrange-Hermite tensor product basis that has already been allocated BASIS_CREATE_START. More... | |
| real(dp) function | basis_routines::basis_lhtp_basis_evaluate_dp (BASIS, NODE_NUMBER, DERIVATIVE_NUMBER, PARTIAL_DERIV_INDEX, XI, ERR, ERROR) |
| Evaluates the double precision Lagrange/Hermite/Fourier tensor product basis function for the given BASIS. More... | |
| subroutine | basis_routines::basis_lhtp_family_create (BASIS, ERR, ERROR,) |
| Creates and initialises a Lagrange-Hermite tensor product basis family that has already been allocated by BASIS_CREATE_START. More... | |
| subroutine | basis_routines::basis_radial_family_create (BASIS, ERR, ERROR,) |
| Creates and initialises a Radial basis family that has already been allocated by BASIS_CREATE_START. More... | |
| subroutine, public | basis_routines::basis_local_node_xi_calculate (BASIS, LOCAL_NODE_NUMBER, XI, ERR, ERROR,) |
| Calculates the xi location of a local node in a basis. More... | |
| subroutine, public | basis_routines::basis_number_of_local_nodes_get (BASIS, NUMBER_OF_LOCAL_NODES, ERR, ERROR,) |
| Returns the number of local nodes in the specified basis. More... | |
| subroutine, public | basis_routines::basis_number_of_xi_get (BASIS, NUMBER_OF_XI, ERR, ERROR,) |
| Gets the number of xi directions for a basis. More... | |
| subroutine | basis_routines::basis_number_of_xi_set_number (USER_NUMBER, NUMBER_OF_XI, ERR, ERROR,) |
| Sets/changes the number of xi directions where the basis is identified by user number. More... | |
| subroutine | basis_routines::basis_number_of_xi_set_ptr (BASIS, NUMBER_OF_XI, ERR, ERROR,) |
| Sets/changes the number of xi directions for a basis identified by a pointer. More... | |
| subroutine | basis_routines::basis_quadrature_create (BASIS, ERR, ERROR,) |
| Creates the quadrature and quadrature schemes on a basis. More... | |
| subroutine, public | basis_routines::basis_quadrature_destroy (QUADRATURE, ERR, ERROR,) |
| Destroys a quadrature on a given basis and deallocates all memory. More... | |
| subroutine | basis_routines::basis_quadrature_finalise (BASIS, ERR, ERROR,) |
| Finalises a quadrature on a given basis and deallocates all memory. More... | |
| subroutine | basis_routines::basis_quadrature_initialise (BASIS, ERR, ERROR,) |
| Initialises a quadrature on the given basis. More... | |
| subroutine, public | basis_routines::basis_quadrature_number_of_gauss_xi_get (BASIS, QUADRATURE_NUMBER_OF_GAUSS_XI, ERR, ERROR,) |
| Get the number of Gauss points in each xi direction on a basis quadrature identified by a pointer. More... | |
| subroutine, public | basis_routines::basis_quadrature_number_of_gauss_xi_set (BASIS, NUMBER_OF_GAUSS_XI, ERR, ERROR,) |
| Sets/changes the number of Gauss points in each xi direction on a basis quadrature identified by a pointer. More... | |
| subroutine, public | basis_routines::basis_quadrature_single_gauss_xi_get (BASIS, SCHEME, GAUSS_POINT, GAUSS_XI, ERR, ERROR,) |
| Returns the xi positions of a Gauss point on a basis quadrature identified by a pointer. More... | |
| subroutine, public | basis_routines::basis_quadrature_multiple_gauss_xi_get (BASIS, SCHEME, GAUSS_POINTS, GAUSS_XI, ERR, ERROR,) |
| Returns the xi positions of Gauss points on a basis quadrature identified by a pointer. If no Gauss points are specified then xi positions of all Gauss points are returned. More... | |
| subroutine, public | basis_routines::basis_quadrature_order_get (BASIS, QUADRATURE_ORDER, ERR, ERROR,) |
| Get the order of a quadrature for a basis quadrature identified by a pointer. More... | |
| subroutine | basis_routines::basis_quadrature_order_set_number (USER_NUMBER, ORDER, ERR, ERROR,) |
| Sets/changes the order of a quadrature for a basis quadrature identified by a user number. More... | |
| subroutine | basis_routines::basis_quadrature_order_set_ptr (BASIS, ORDER, ERR, ERROR,) |
| Sets/changes the order of a quadrature for a basis quadrature identified by a pointer. More... | |
| subroutine, public | basis_routines::basis_quadrature_type_get (BASIS, QUADRATURE_TYPE, ERR, ERROR,) |
| get the quadrature type on a basis identified by a pointer. More... | |
| subroutine | basis_routines::basis_quadrature_type_set_number (USER_NUMBER, TYPE, ERR, ERROR,) |
| Sets/changes the quadrature type for a basis quadrature identified by a user number. More... | |
| subroutine | basis_routines::basis_quadrature_type_set_ptr (BASIS, TYPE, ERR, ERROR,) |
| Sets/changes the quadrature type on a basis identified by a pointer. More... | |
| subroutine, public | basis_routines::basis_quadraturelocalfacegaussevaluateset (BASIS, FACE_GAUSS_EVALUATE, ERR, ERROR,) |
| Sets/changes the local face Gauss evaluation flag on a basis. More... | |
| subroutine | basis_routines::basis_simplex_basis_create (BASIS, ERR, ERROR,) |
| Creates and initialises a simplex basis that has already been allocated BASIS_CREATE_START. More... | |
| subroutine | basis_routines::basis_simplex_family_create (BASIS, ERR, ERROR,) |
| Creates and initialises a simplex basis family that has already been allocated by BASIS_CREATE_START. More... | |
| real(dp) function | basis_routines::basis_simplex_basis_evaluate (BASIS, NODE_NUMBER, PARTIAL_DERIV_INDEX, XL, ERR, ERROR) |
Evaluates a simplex basis function and its derivatives with respect to external 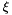 coordinates. For Simplex line elements there are two area coordinates which are a function of coordinates. For Simplex line elements there are two area coordinates which are a function of 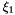 : :  and and 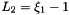 .The derivatives wrt to external coordinates are then given by .The derivatives wrt to external coordinates are then given by 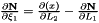 and and 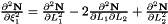 . For Simplex triangle elements there are three area coordinates which are a function of . For Simplex triangle elements there are three area coordinates which are a function of 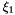 and and 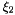 : :  , , 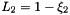 and and 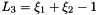 . The derivatives wrt to external coordinates are then given by . The derivatives wrt to external coordinates are then given by 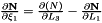 , , 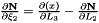 , , 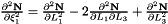 , , 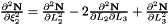 and and 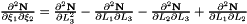 . For Simplex tetrahedral elements there are four area coordinates which are a function of . For Simplex tetrahedral elements there are four area coordinates which are a function of 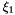 , , 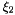 and and 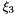 : :  , , 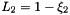 , , 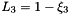 and and 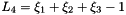 . The derivatives wrt to external coordinates are then given by . The derivatives wrt to external coordinates are then given by 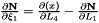 , , 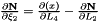 , , 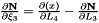 , , 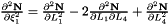 , , 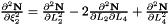 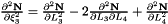 , , 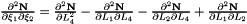 , , 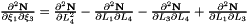 , , 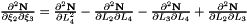 and and 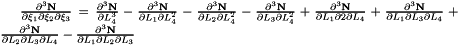 . More... . More... | |
| real(dp) function | basis_routines::basis_simplex_basis_derivative_evaluate (BASIS, NODE_NUMBER, PARTIAL_DERIV_INDEX, XL, ERR, ERROR) |
| Evaluates partial derivatives of a simplex basis function with respect to area coordinates. More... | |
| subroutine | basis_routines::basis_sub_basis_create (PARENT_BASIS, NUMBER_OF_XI, XI_DIRECTIONS, SUB_BASIS, ERR, ERROR,) |
| Creates a sub-basis on a parent basis. More... | |
| subroutine, public | basis_routines::basis_type_get (BASIS, TYPE, ERR, ERROR,) |
| get the type for a basis is identified by a a pointer. More... | |
| subroutine | basis_routines::basis_type_set_number (USER_NUMBER, TYPE, ERR, ERROR,) |
| Sets/changes the type for a basis is identified by a user number. More... | |
| subroutine | basis_routines::basis_type_set_ptr (BASIS, TYPE, ERR, ERROR,) |
| Sets/changes the type for a basis is identified by a a pointer. More... | |
| subroutine, public | basis_routines::basis_collapsed_xi_get (BASIS, COLLAPSED_XI, ERR, ERROR,) |
| Gets the collapsed xi flags for a basis is identified by a a pointer. More... | |
| subroutine | basis_routines::basis_collapsed_xi_set_number (USER_NUMBER, COLLAPSED_XI, ERR, ERROR,) |
| Sets/changes the collapsed xi flags for a basis is identified by a user number. More... | |
| subroutine | basis_routines::basis_collapsed_xi_set_ptr (BASIS, COLLAPSED_XI, ERR, ERROR,) |
| Sets/changes the collapsed xi flags for a basis is identified by a a pointer. More... | |
| subroutine, public | basis_routines::basis_user_number_find (USER_NUMBER, BASIS, ERR, ERROR,) |
| Finds and returns in BASIS a pointer to the basis with the number given in USER_NUMBER. If no basis with that number exits BASIS is left nullified. More... | |
| subroutine | basis_routines::gauss_legendre (N, ALPHA, BETA, X, W, ERR, ERROR,) |
| This routine calculates the weights and abscissae for a Gauss-Legendre quadrature scheme. More... | |
| subroutine | basis_routines::gauss_simplex (ORDER, NUMBER_OF_VERTICES, N, X, W, ERR, ERROR,) |
| This routine calculates the weights and abscissae for a Gauss quadrature scheme for simplex elements. More... | |
| real(dp) function | basis_routines::hermite_cubic_evaluate (NODE_INDEX, NODE_DERIVATIVE_INDEX, PARTIAL_DERIVATIVE_INDEX, XI, ERR, ERROR) |
| Evaluates a 1D cubic Hermite basis function. More... | |
| real(dp) function | basis_routines::hermite_quadratic_evaluate (NODE_INDEX, NODE_DERIVATIVE_INDEX, PARTIAL_DERIVATIVE_INDEX, SPECIAL_NODE_INDEX, XI, ERR, ERROR) |
| Evaluates a 1D quadratic Hermite basis function. More... | |
| real(dp) function | basis_routines::lagrange_cubic_evaluate (NODE_INDEX, PARTIAL_DERIVATIVE_INDEX, XI, ERR, ERROR) |
| Evaluates a 1D cubic Lagrange basis function. More... | |
| real(dp) function | basis_routines::lagrange_linear_evaluate (NODE_INDEX, PARTIAL_DERIVATIVE_INDEX, XI, ERR, ERROR) |
| Evaluates a 1D linear Lagrange basis function. More... | |
| real(dp) function | basis_routines::lagrange_quadratic_evaluate (NODE_INDEX, PARTIAL_DERIVATIVE_INDEX, XI, ERR, ERROR) |
| Evaluates a 1D quadratic Lagrange basis function. More... | |
| real(dp) function | basis_routines::simplex_cubic_evaluate_dp (NODE_INDEX, PARTIAL_DERIVATIVE_INDEX, XL, ERR, ERROR) |
| Evaluates a cubic simpelx basis function at a specificed area position and node index and with a given partial derivative index with respect to area coordinates for double precision arguments. More... | |
| real(dp) function | basis_routines::simplex_linear_evaluate_dp (NODE_INDEX, PARTIAL_DERIVATIVE_INDEX, XL, ERR, ERROR) |
| Evaluates a linear simpelx basis function at a specificed area position and node index and with a given partial derivative index with respect to area coordinates for double precision arguments. More... | |
| real(dp) function | basis_routines::simplex_quadratic_evaluate_dp (NODE_INDEX, PARTIAL_DERIVATIVE_INDEX, XL, ERR, ERROR) |
| Evaluates a quadratic simpelx basis function at a specificed area position and node index and with a given partial derivative index with respect to area coordinates for double precision arguments. More... | |
Variables | |
| integer(intg), parameter, public | basis_routines::basis_lagrange_hermite_tp_type =1 |
| Lagrange-Hermite tensor product basis type. More... | |
| integer(intg), parameter, public | basis_routines::basis_simplex_type =2 |
| Simplex basis type. More... | |
| integer(intg), parameter, public | basis_routines::basis_serendipity_type =3 |
| Serendipity basis type. More... | |
| integer(intg), parameter, public | basis_routines::basis_auxilliary_type =4 |
| Auxillary basis type. More... | |
| integer(intg), parameter, public | basis_routines::basis_b_spline_tp_type =5 |
| B-spline basis type. More... | |
| integer(intg), parameter, public | basis_routines::basis_fourier_lagrange_hermite_tp_type =6 |
| Fourier-Lagrange tensor product basis type. More... | |
| integer(intg), parameter, public | basis_routines::basis_extended_lagrange_tp_type =7 |
| Extendend Lagrange tensor product basis type. More... | |
| integer(intg), parameter, public | basis_routines::basis_radial_type =7 |
| Radial basis typee. More... | |
| integer(intg), parameter, public | basis_routines::basis_linear_lagrange_interpolation =1 |
| Linear Lagrange interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_quadratic_lagrange_interpolation =2 |
| Quadratic Lagrange interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_cubic_lagrange_interpolation =3 |
| Cubic Lagrange interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_cubic_hermite_interpolation =4 |
| Cubic Hermite interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_quadratic1_hermite_interpolation =5 |
| Quadratic Hermite (no derivative at xi=0) interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_quadratic2_hermite_interpolation =6 |
| Quadratic Hermite (no derivative at xi=1) interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_linear_simplex_interpolation =7 |
| Linear Simplex interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_quadratic_simplex_interpolation =8 |
| Quadratic Simplex interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_cubic_simplex_interpolation =9 |
| Cubic Simplex interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_gaussian_radial_interpolation =10 |
| Gaussian Radial interpolation specification. More... | |
| integer(intg), parameter, public | basis_routines::basis_multiquartic_radial_interpolation =11 |
| Multiquartic Radial interpolation specification. More... | |
| integer(intg), parameter | basis_routines::basis_lagrange_interpolation =1 |
| Lagrange interpolation. More... | |
| integer(intg), parameter | basis_routines::basis_hermite_interpolation =2 |
| Hermite interpolation. More... | |
| integer(intg), parameter | basis_routines::basis_simplex_interpolation =3 |
| Simplex interpolation. More... | |
| integer(intg), parameter | basis_routines::basis_serendipity_interpolation =4 |
| Serendipity interpolation. More... | |
| integer(intg), parameter | basis_routines::basis_transition_interpolation =5 |
| Transition interpolation. More... | |
| integer(intg), parameter | basis_routines::basis_singular_interpolation =6 |
| Singular interpolation. More... | |
| integer(intg), parameter | basis_routines::basis_fourier_interpolation =7 |
| Fourier interpolation. More... | |
| integer(intg), parameter | basis_routines::basis_radial_interpolation =8 |
| Radial interpolation. More... | |
| integer(intg), parameter, public | basis_routines::basis_linear_interpolation_order =1 |
| Linear interpolation order. More... | |
| integer(intg), parameter, public | basis_routines::basis_quadratic_interpolation_order =2 |
| Quadratic interpolation order. More... | |
| integer(intg), parameter, public | basis_routines::basis_cubic_interpolation_order =3 |
| Cubic interpolation order. More... | |
| integer(intg), parameter, public | basis_routines::basis_quadratic1_interpolation_order =4 |
| Quadratic (no derivative at xi=0) interpolation order. More... | |
| integer(intg), parameter, public | basis_routines::basis_quadratic2_interpolation_order =5 |
| Quadratic (no derivative at xi=1) interpolation order. More... | |
| integer(intg), parameter | basis_routines::basis_number_of_quadrature_scheme_types =4 |
| The number of currently defined quadrature schemes. More... | |
| integer(intg), parameter, public | basis_routines::basis_default_quadrature_scheme =1 |
| Identifier for the default quadrature scheme. More... | |
| integer(intg), parameter, public | basis_routines::basis_low_quadrature_scheme =2 |
| Identifier for a low order quadrature scheme. More... | |
| integer(intg), parameter, public | basis_routines::basis_mid_quadrature_scheme =3 |
| Identifier for a mid order quadrature scheme. More... | |
| integer(intg), parameter, public | basis_routines::basis_high_quadrature_scheme =4 |
| Identifier for a high order quadrature scheme. More... | |
| integer(intg), parameter, public | basis_routines::basis_gauss_legendre_quadrature =1 |
| Gauss-Legendre quadrature. More... | |
| integer(intg), parameter, public | basis_routines::basis_gauss_laguerre_quadrature =2 |
| Gauss-Laguerre quadrature. More... | |
| integer(intg), parameter, public | basis_routines::basis_guass_hermite_quadrature =3 |
| Gauss-Hermite quadrature. More... | |
| integer(intg), parameter, public | basis_routines::basis_adaptive_gauss_legendre_quadrature =4 |
| Adaptive Gauss-Legendre quadrature. More... | |
| integer(intg), parameter, public | basis_routines::basis_gauss_simplex_quadrature =5 |
| Gauss-Legendre for Simplex elements quadrature. More... | |
| integer(intg), parameter, public | basis_routines::basis_xi_collapsed =1 |
| The Xi direction is collapsed. More... | |
| integer(intg), parameter, public | basis_routines::basis_collapsed_at_xi0 =2 |
| The Xi direction at the xi=0 end of this Xi direction is collapsed. More... | |
| integer(intg), parameter, public | basis_routines::basis_collapsed_at_xi1 =3 |
| The Xi direction at the xi=1 end of this Xi direction is collapsed. More... | |
| integer(intg), parameter, public | basis_routines::basis_not_collapsed =4 |
| The Xi direction is not collapsed. More... | |
| type(basis_functions_type), public | basis_routines::basis_functions |
| The tree of defined basis functions. More... | |
Detailed Description
This module contains all basis function routines.
LICENSE
Version: MPL 1.1/GPL 2.0/LGPL 2.1
The contents of this file are subject to the Mozilla Public License Version 1.1 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.mozilla.org/MPL/
Software distributed under the License is distributed on an "AS IS" basis, WITHOUT WARRANTY OF ANY KIND, either express or implied. See the License for the specific language governing rights and limitations under the License.
The Original Code is OpenCMISS
The Initial Developer of the Original Code is University of Auckland, Auckland, New Zealand, the University of Oxford, Oxford, United Kingdom and King's College, London, United Kingdom. Portions created by the University of Auckland, the University of Oxford and King's College, London are Copyright (C) 2007-2010 by the University of Auckland, the University of Oxford and King's College, London. All Rights Reserved.
Contributor(s):
Alternatively, the contents of this file may be used under the terms of either the GNU General Public License Version 2 or later (the "GPL"), or the GNU Lesser General Public License Version 2.1 or later (the "LGPL"), in which case the provisions of the GPL or the LGPL are applicable instead of those above. If you wish to allow use of your version of this file only under the terms of either the GPL or the LGPL, and not to allow others to use your version of this file under the terms of the MPL, indicate your decision by deleting the provisions above and replace them with the notice and other provisions required by the GPL or the LGPL. If you do not delete the provisions above, a recipient may use your version of this file under the terms of any one of the MPL, the GPL or the LGPL.
Definition in file basis_routines.f90.
