This module contains all program wide constants. More...
Variables | |
| real(dp), parameter | euler =2.718281828459045235360287471352662497757_DP |
| The double precision value of e. More... | |
| real(dp), parameter | pi =3.141592653589793238462643383279502884197_DP |
| The double precision value of pi. More... | |
| real(dp), parameter | twopi =6.283185307179586476925286766559005768394_DP |
| The double value of 2pi. More... | |
| real(dp), parameter | convergence_tolerance_dp =5.0_DP*EPSILON(1.0_DP) |
The convergence tolerance for double precision convergence calculations. Convergence tests should be of the form 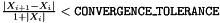 or for norms, or for norms, 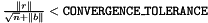 . More... . More... | |
| real(dp), parameter | convergence_tolerance =CONVERGENCE_TOLERANCE_DP |
| real(dp) | loose_tolerance |
| The loose tolerance for double precision convergence calculations. Loose tolerance is to be used in the same manner as CONSTANTS::CONVERGENCE_TOLERANCE when a looser criterion is desired. More... | |
| real(dp), parameter | zero_tolerance_dp =5.0_DP*EPSILON(1.0_DP) |
| The zero tolerance for double precision zero tests i.e., if(abs(x)>zero_tolerance) then... More... | |
| real(dp), parameter | zero_tolerance =ZERO_TOLERANCE_DP |
| real(dp), parameter | convergence_tolerance_sp =5.0_SP*EPSILON(1.0_SP) |
The convergence tolerance for single precision convergence calculations. Convergence tests should be of the form 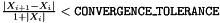 or for norms, or for norms, 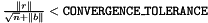 . More... . More... | |
| real(sp) | loose_tolerance_sp |
| The loose tolerance for single precision convergence calculations. Loose tolerance is to be used in the same manner as CONSTANTS::CONVERGENCE_TOLERANCE_SP when a looser criterion is desired. More... | |
| real(sp), parameter | zero_tolerance_sp =5.0_SP*EPSILON(1.0_SP) |
| The zero tolerance for single precision zero tests i.e., if(abs(x)>zero_tolerance) then... More... | |
| integer(intg), parameter | maxstrlen =255 |
| Maximum string length fro character strings. More... | |
| integer(intg), parameter | integer_type =1 |
| Integer data type. More... | |
| integer(intg), parameter | short_integer_type =2 |
| Short integer data type. More... | |
| integer(intg), parameter | long_integer_type =3 |
| Long integer data type. More... | |
| integer(intg), parameter | single_real_type =4 |
| Single precision real data type. More... | |
| integer(intg), parameter | double_real_type =5 |
| Double precision real data type. More... | |
| integer(intg), parameter | quadruple_real_type =6 |
| Quadruple precision real data type. More... | |
| integer(intg), parameter | character_type =7 |
| Character data type. More... | |
| integer(intg), parameter | logical_type =8 |
| Logical/boolean data type. More... | |
| integer(intg), parameter | single_complex_type =9 |
| Single precision complex data type. More... | |
| integer(intg), parameter | double_complex_type =10 |
| Double precision complex data type. More... | |
| integer(intg), parameter | quadruple_complex_type =11 |
| Quadruple precision complex data type. More... | |
| integer(intg), parameter | c_int_type =12 |
| C integer data type. More... | |
| integer(intg), parameter | big_endian_number =1 |
| Big endian number type. More... | |
| integer(intg), parameter | little_endian_number =2 |
| Little endian number type. More... | |
| integer(intg), parameter | ascii_character =1 |
| ASCII character type. More... | |
| integer(intg), parameter | unicode_character =2 |
| Unicode character type. More... | |
| integer(intg), parameter | twos_complement_integer =1 |
| Twos complement integer type. More... | |
| integer(intg), parameter | signed_magnitude_integer =2 |
| Signed magnitude integer type. More... | |
| integer(intg), parameter | spieee_number =1 |
| Single precision IEEE real type. More... | |
| integer(intg), parameter | dpieee_number =2 |
| Double precision IEEE real type. More... | |
| integer(intg), parameter | dec_computer =1 |
| Digital computer system type. More... | |
| integer(intg), parameter | sgi_computer =2 |
| Silicon Graphics computer system type. More... | |
| integer(intg), parameter | ibm_computer =3 |
| IBM system type. More... | |
| integer(intg), parameter | cray_computer =4 |
| Cray computer system type. More... | |
| integer(intg), parameter | pc_computer =5 |
| PC computer system type. More... | |
| integer(intg), parameter | unknown_computer =255 |
| Unknown computer system type. More... | |
| integer(intg), parameter | vms_os =1 |
| VMS operating system type. More... | |
| integer(intg), parameter | irix_os =2 |
| IRIX operating system type. More... | |
| integer(intg), parameter | windows_os =3 |
| Windows operating system type. More... | |
| integer(intg), parameter | linux_os =4 |
| Linux operating system type. More... | |
| integer(intg), parameter | aix_os =5 |
| AIX operating system type. More... | |
| integer(intg), parameter | unknown_os =255 |
| Unknown operating system type. More... | |
| integer(intg), parameter | library_cmiss_type =1 |
| CMISS (internal) library type. More... | |
| integer(intg), parameter | library_petsc_type =2 |
| PETSc library type. More... | |
| integer(intg), parameter | library_mumps_type =3 |
| MUMPS library type. More... | |
| integer(intg), parameter | library_superlu_type =4 |
| SuperLU library type. More... | |
| integer(intg), parameter | library_spooles_type =5 |
| SPOOLES library type. More... | |
| integer(intg), parameter | library_umfpack_type =6 |
| UMFPack library type. More... | |
| integer(intg), parameter | library_lusol_type =7 |
| LUSOL library type. More... | |
| integer(intg), parameter | library_essl_type =8 |
| ESSL library type. More... | |
| integer(intg), parameter | library_lapack_type =9 |
| LAPACK library type. More... | |
| integer(intg), parameter | library_tao_type =10 |
| TAO library type. More... | |
| integer(intg), parameter | library_hypre_type =11 |
| Hypre library type. More... | |
| integer(intg), parameter | library_pastix_type =12 |
| PaStiX library type. More... | |
| integer(intg), parameter | no_part_deriv =1 |
| No partial derivative i.e., u. More... | |
| integer(intg), parameter | first_part_deriv =2 |
| First partial derivative i.e., du/ds. More... | |
| integer(intg), parameter | second_part_deriv =3 |
| Second partial derivative i.e., d^2u/ds^2. More... | |
| integer(intg), parameter | third_part_deriv =4 |
| Third partial derivative i.e., d^3u/ds^3. More... | |
| integer(intg), parameter | part_deriv_s1 =2 |
| First partial derivative in the s1 direction i.e., du/ds1. More... | |
| integer(intg), parameter | part_deriv_s1_s1 =3 |
| Second partial derivative in the s1 direction i.e., d^2u/ds1ds1. More... | |
| integer(intg), parameter | part_deriv_s2 =4 |
| First partial derivative in the s2 direction i.e., du/ds2. More... | |
| integer(intg), parameter | part_deriv_s2_s2 =5 |
| Second partial derivative in the s2 direction i.e., d^2u/ds2ds2. More... | |
| integer(intg), parameter | part_deriv_s1_s2 =6 |
| Cross derivative in the s1 and s2 direction i.e., d^2u/ds1ds2. More... | |
| integer(intg), parameter | part_deriv_s3 =7 |
| First partial derivative in the s3 direction i.e., du/ds3. More... | |
| integer(intg), parameter | part_deriv_s3_s3 =8 |
| Second partial derivative in the s3 direction i.e., d^2u/ds3ds3. More... | |
| integer(intg), parameter | part_deriv_s1_s3 =9 |
| Cross derivative in the s1 and s3 direction i.e., d^2u/ds1ds3. More... | |
| integer(intg), parameter | part_deriv_s2_s3 =10 |
| Cross derivative in the s2 and s3 direction i.e., d^2u/ds2ds3. More... | |
| integer(intg), parameter | part_deriv_s1_s2_s3 =11 |
| Cross derivative in the s1, s2 and s3 direction i.e., d^3u/ds1ds2ds3. More... | |
| integer(intg), parameter | part_deriv_s4 =12 |
| First partial derivative in the s4 direction i.e., du/ds4. More... | |
| integer(intg), parameter | part_deriv_s4_s4 =13 |
| Second partial derivative in the s4 direction i.e., d^2u/ds4ds4. More... | |
| integer(intg), parameter | part_deriv_s1_s4 =14 |
| Cross derivative in the s1 and s4 direction i.e., d^2u/ds1ds4. More... | |
| integer(intg), parameter | part_deriv_s2_s4 =15 |
| Cross derivative in the s2 and s4 direction i.e., d^2u/ds2ds4. More... | |
| integer(intg), parameter | part_deriv_s3_s4 =16 |
| Cross derivative in the s3 and s4 direction i.e., d^2u/ds3ds4. More... | |
| integer(intg), parameter | part_deriv_s1_s2_s4 =17 |
| Cross derivative in the s1, s2 and s4 direction i.e., d^3u/ds1ds2ds4. More... | |
| integer(intg), parameter | part_deriv_s1_s3_s4 =18 |
| Cross derivative in the s1, s3 and s4 direction i.e., d^3u/ds1ds3ds4. More... | |
| integer(intg), parameter | part_deriv_s2_s3_s4 =19 |
| Cross derivative in the s2, s3 and s4 direction i.e., d^3u/ds2ds3ds4. More... | |
| integer(intg), parameter | part_deriv_s1_s4_s4 =20 |
| Cross derivative in the s2, s4 and s4 direction i.e., d^3u/ds1ds4^2. More... | |
| integer(intg), parameter | part_deriv_s2_s4_s4 =21 |
| Cross derivative in the s2, s4 and s4 direction i.e., d^3u/ds2ds4^2. More... | |
| integer(intg), parameter | part_deriv_s3_s4_s4 =22 |
| Cross derivative in the s3, s4 and s4 direction i.e., d^3u/ds3ds4^2. More... | |
| integer(intg), parameter | part_deriv_s4_s4_s4 =23 |
| Third partial derivative in the s4 direction i.e., d^3u/ds4^3. More... | |
| integer(intg), parameter | maximum_global_deriv_number =8 |
| The maximum global derivative number. More... | |
| integer(intg), parameter | no_global_deriv =1 |
| No global derivative i.e., u. More... | |
| integer(intg), parameter | global_deriv_s1 =2 |
| First global derivative in the s1 direction i.e., du/ds1. More... | |
| integer(intg), parameter | global_deriv_s2 =3 |
| First global derivative in the s2 direction i.e., du/ds2. More... | |
| integer(intg), parameter | global_deriv_s1_s2 =4 |
| Global Cross derivative in the s1 and s2 direction i.e., d^2u/ds1ds2. More... | |
| integer(intg), parameter | global_deriv_s3 =5 |
| First global derivative in the s3 direction i.e., du/ds3. More... | |
| integer(intg), parameter | global_deriv_s1_s3 =6 |
| Global Cross derivative in the s1 and s3 direction i.e., d^2u/ds1ds3. More... | |
| integer(intg), parameter | global_deriv_s2_s3 =7 |
| Global Cross derivative in the s2 and s3 direction i.e., d^2u/ds2ds3. More... | |
| integer(intg), parameter | global_deriv_s1_s2_s3 =8 |
| Cross derivative in the s1, s2 and s3 direction i.e., d^3u/ds1ds2ds3. More... | |
| integer(intg), parameter | maximum_physical_deriv_number =2 |
| The maximum physical derivative number. More... | |
| integer(intg), parameter | no_physical_deriv =1 |
| No physical derivative i.e., u. More... | |
| integer(intg), parameter | gradient_physical_deriv =2 |
| Gradient physical derivative i.e., grad u. More... | |
| integer(intg), dimension(23, 4) | partial_derivative_index = RESHAPE( [ NO_PART_DERIV,FIRST_PART_DERIV,SECOND_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV, FIRST_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV,NO_PART_DERIV, FIRST_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,FIRST_PART_DERIV,FIRST_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV, NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV,SECOND_PART_DERIV, FIRST_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV, FIRST_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV, NO_PART_DERIV,FIRST_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV,NO_PART_DERIV, FIRST_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,FIRST_PART_DERIV,SECOND_PART_DERIV,FIRST_PART_DERIV,FIRST_PART_DERIV, FIRST_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV, FIRST_PART_DERIV,NO_PART_DERIV,FIRST_PART_DERIV,FIRST_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,FIRST_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV,NO_PART_DERIV, NO_PART_DERIV,FIRST_PART_DERIV,SECOND_PART_DERIV,FIRST_PART_DERIV,FIRST_PART_DERIV, FIRST_PART_DERIV,FIRST_PART_DERIV,FIRST_PART_DERIV,FIRST_PART_DERIV,SECOND_PART_DERIV, SECOND_PART_DERIV,SECOND_PART_DERIV,THIRD_PART_DERIV ], [23,4]) |
| Partial derivative index map. PARTIAL_DERIVATIVE_INDEX(idx,nic) gives the order of the partial derivative in the ni(c)'th direction for the idx'th partial derivative value. More... | |
| integer(intg), dimension(4) | partial_derivative_first_derivative_map = [ PART_DERIV_S1,PART_DERIV_S2,PART_DERIV_S3,PART_DERIV_S4 ] |
| PARTIAL_DERIVATIVE_FIRST_DERIVATIVE_MAP(nic) gives the partial derivative index for the first derivative in the ni(c)'th direction. More... | |
| integer(intg), dimension(4) | partial_derivative_second_derivative_map = [ PART_DERIV_S1_S1,PART_DERIV_S2_S2,PART_DERIV_S3_S3, PART_DERIV_S4_S4 ] |
| PARTIAL_DERIVATIVE_SECOND_DERIVATIVE_MAP(nic) gives the partial derivative index for the second derivative in the ni(c)'th direction. More... | |
| integer(intg), dimension(4) | partial_derivative_maximum_map = [ PART_DERIV_S1_S1,PART_DERIV_S1_S2,PART_DERIV_S1_S2_S3, PART_DERIV_S4_S4_S4 ] |
| PARTIAL_DERIVATIVE_MAXIMUM_MAP(nic) gives the maximum of partial derivative index for the the ni(c)'th direction. More... | |
| integer(intg), dimension(20) | partial_derivative_global_derivative_map = [ NO_GLOBAL_DERIV,GLOBAL_DERIV_S1,0,GLOBAL_DERIV_S2,0, GLOBAL_DERIV_S1_S2,GLOBAL_DERIV_S3,0,GLOBAL_DERIV_S1_S3,GLOBAL_DERIV_S2_S3,GLOBAL_DERIV_S1_S2_S3,0,0,0,0,0,0,0,0,0 ] |
| PARTIAL_DERIVATIVE_GLOBAL_DERIVATIVE_MAP(nu) gives the global derivative index for the the nu'th partial derivative. If no global derivative exists the map is zero. More... | |
| integer(intg), dimension(8) | global_derivative_partial_derivative_map = [ NO_PART_DERIV,PART_DERIV_S1,PART_DERIV_S2,PART_DERIV_S1_S2, PART_DERIV_S3,PART_DERIV_S1_S3,PART_DERIV_S2_S3,PART_DERIV_S1_S2_S3] |
| GLOBAL_DERIVATIVE_PARTIAL_DERIVATIVE_MAP(nk) gives the partial derivative index for the the nk'th global derivative. More... | |
| integer(intg), dimension(3) | global_derivative_maximum_map = [ GLOBAL_DERIV_S1,GLOBAL_DERIV_S1_S2,GLOBAL_DERIV_S1_S2_S3 ] |
| GLOBAL_DERIVATIVE_MAXIMUM_MAP(ni) gives the maximum of global derivative index for the the ni'th direction. More... | |
| integer(intg), dimension(2) | other_xi_directions2 = [ 2,1 ] |
| OTHER_XI_DIRECTIONS2(ni) gives the other xi direction for direction ni for a two dimensional element. More... | |
| integer(intg), dimension(3, 3, 2) | other_xi_directions3 = RESHAPE([ 1,2,3,2,1,1,3,3,2,0,3,2,3,0,1,2,1,0 ], [3,3,2]) |
| OTHER_XI_DIRECTIONS3(ni,nii,type) gives the other xi directions for direction ni for a three dimensional element. When type=1 then the nii index gives the other two xi directions (for nii=2,3) and when type=2 then ni and nii are used to give the third xi direction. More... | |
| integer(intg), dimension(4, 3) | other_xi_directions4 = RESHAPE([ 2,3,4,1,3,4,1,2,4,1,2,3 ], [4,3]) |
| OTHER_XI_DIRECTIONS4(nic,nii) gives the other xi coordinates for coordinate nic for a simplex element. More... | |
| integer(intg), dimension(2) | other_xi_orientations2 = [1,-1] |
| OTHER_XI_ORIENTATIONSS2(ni) gives the orientation of the given xi direction and the other xi direction. Is equal to leviCivita(ni,OTHER_XI_DIRECTIONS2(ni)) where leviCivita is the Levi-Civita or alternating symbol. More... | |
| integer(intg), dimension(3, 3) | other_xi_orientations3 = RESHAPE([0,-1,1,1,0,-1,-1,1,0], [3,3]) |
| OTHER_XI_ORIENTATIONSS3(ni,nii) gives the orientation of the given two xi directions. Is equal to leviCivita(ni,nii,OTHER_XI_DIRECTIONS3(ni,nii,2)) where leviCivita is the Levi-Civita or alternating symbol. More... | |
| integer(intg), dimension(2, 2), parameter | tensor_to_voigt2 =RESHAPE([1,3,3,2], [2,2]) |
| integer(intg), dimension(2, 3), parameter | voigt_to_tensor2 =RESHAPE([1,1,2,2,1,2], [2,3]) |
| integer(intg), dimension(3, 3), parameter | tensor_to_voigt3 =RESHAPE([1,4,5,4,2,6,5,6,3], [3,3]) |
| integer(intg), dimension(2, 6), parameter | voigt_to_tensor3 =RESHAPE([1,1,2,2,3,3,1,2,1,3,2,3], [2,6]) |
Detailed Description
This module contains all program wide constants.
Variable Documentation
| integer(intg), dimension(3) constants::global_derivative_maximum_map = [ GLOBAL_DERIV_S1,GLOBAL_DERIV_S1_S2,GLOBAL_DERIV_S1_S2_S3 ] |
GLOBAL_DERIVATIVE_MAXIMUM_MAP(ni) gives the maximum of global derivative index for the the ni'th direction.
Definition at line 269 of file constants.f90.
| integer(intg), dimension(8) constants::global_derivative_partial_derivative_map = [ NO_PART_DERIV,PART_DERIV_S1,PART_DERIV_S2,PART_DERIV_S1_S2, PART_DERIV_S3,PART_DERIV_S1_S3,PART_DERIV_S2_S3,PART_DERIV_S1_S2_S3] |
GLOBAL_DERIVATIVE_PARTIAL_DERIVATIVE_MAP(nk) gives the partial derivative index for the the nk'th global derivative.
Definition at line 265 of file constants.f90.
| integer(intg), parameter constants::maxstrlen =255 |
Maximum string length fro character strings.
Definition at line 79 of file constants.f90.
Referenced by base_routines::base_routines_initialise(), fieldml_input_routines::fieldml_input_get_basis_info(), fieldml_input_routines::fieldml_input_initialise_from_file(), fieldml_input_routines::fieldml_input_is_known_basis(), fieldml_output_routines::fieldml_output_get_simple_basis_name(), fieldml_output_routines::fieldml_output_get_simple_layout_name(), fieldml_output_routines::fieldml_output_get_type_argument_handle(), fieldml_output_routines::fieldml_output_import_handle(), fieldml_input_routines::fieldmlinput_coordinatesystemcreatestart(), strings::list_to_character_c(), strings::list_to_character_dp(), strings::list_to_character_intg(), strings::list_to_character_l(), strings::list_to_character_lintg(), strings::list_to_character_sp(), strings::number_to_character_dp(), strings::number_to_character_sp(), strings::number_to_vstring_dp(), and strings::number_to_vstring_sp().
| integer(intg), dimension(2) constants::other_xi_directions2 = [ 2,1 ] |
OTHER_XI_DIRECTIONS2(ni) gives the other xi direction for direction ni for a two dimensional element.
Definition at line 273 of file constants.f90.
Referenced by basis_routines::basis_collapsed_xi_set_ptr(), and basis_routines::basis_lhtpbasiscreate().
| integer(intg), dimension(3,3,2) constants::other_xi_directions3 = RESHAPE([ 1,2,3,2,1,1,3,3,2,0,3,2,3,0,1,2,1,0 ], [3,3,2]) |
OTHER_XI_DIRECTIONS3(ni,nii,type) gives the other xi directions for direction ni for a three dimensional element. When type=1 then the nii index gives the other two xi directions (for nii=2,3) and when type=2 then ni and nii are used to give the third xi direction.
Definition at line 275 of file constants.f90.
Referenced by basis_routines::basis_collapsed_xi_set_ptr(), basis_routines::basis_lhtp_family_create(), basis_routines::basis_lhtpbasiscreate(), basis_routines::basis_quadrature_create(), basis_routines::basis_simplex_family_create(), finite_elasticity_routines::finiteelasticity_surfacepressurejacobianevaluate(), and finite_elasticity_routines::finiteelasticity_surfacepressureresidualevaluate().
| integer(intg), dimension(4,3) constants::other_xi_directions4 = RESHAPE([ 2,3,4,1,3,4,1,2,4,1,2,3 ], [4,3]) |
OTHER_XI_DIRECTIONS4(nic,nii) gives the other xi coordinates for coordinate nic for a simplex element.
Definition at line 277 of file constants.f90.
| integer(intg), dimension(2) constants::other_xi_orientations2 = [1,-1] |
OTHER_XI_ORIENTATIONSS2(ni) gives the orientation of the given xi direction and the other xi direction. Is equal to leviCivita(ni,OTHER_XI_DIRECTIONS2(ni)) where leviCivita is the Levi-Civita or alternating symbol.
Definition at line 279 of file constants.f90.
| integer(intg), dimension(3,3) constants::other_xi_orientations3 = RESHAPE([0,-1,1,1,0,-1,-1,1,0], [3,3]) |
OTHER_XI_ORIENTATIONSS3(ni,nii) gives the orientation of the given two xi directions. Is equal to leviCivita(ni,nii,OTHER_XI_DIRECTIONS3(ni,nii,2)) where leviCivita is the Levi-Civita or alternating symbol.
Definition at line 280 of file constants.f90.
Referenced by finite_elasticity_routines::finiteelasticity_surfacepressurejacobianevaluate(), and finite_elasticity_routines::finiteelasticity_surfacepressureresidualevaluate().
| integer(intg), dimension(4) constants::partial_derivative_first_derivative_map = [ PART_DERIV_S1,PART_DERIV_S2,PART_DERIV_S3,PART_DERIV_S4 ] |
PARTIAL_DERIVATIVE_FIRST_DERIVATIVE_MAP(nic) gives the partial derivative index for the first derivative in the ni(c)'th direction.
Definition at line 254 of file constants.f90.
Referenced by advection_diffusion_equation_routines::advectiondiffusion_finiteelementcalculate(), biodomain_equation_routines::biodomain_equation_finite_element_calculate(), burgers_equation_routines::burgers_finiteelementjacobianevaluate(), burgers_equation_routines::burgers_finiteelementresidualevaluate(), coordinate_routines::coordinate_metrics_calculate(), coordinate_routines::coordinate_system_normal_calculate(), darcy_equations_routines::darcy_equation_finite_element_calculate(), darcy_equations_routines::darcy_equation_impermeable_bc_via_penalty(), darcy_pressure_equations_routines::darcypressure_finiteelementresidualevaluate(), diffusion_equation_routines::diffusion_equation_finite_element_calculate(), diffusion_equation_routines::diffusion_finiteelementresidualevaluate(), finite_elasticity_routines::finite_elasticity_gauss_dfdz(), finite_elasticity_routines::finiteelasticity_finiteelementjacobianevaluate(), finite_elasticity_routines::finiteelasticity_finiteelementresidualevaluate(), finite_elasticity_routines::finiteelasticity_surfacepressurejacobianevaluate(), fitting_routines::fitting_finite_element_calculate(), fitting_routines::fitting_gauss_deformation_gradient_tensor(), helmholtz_equations_routines::HELMHOLTZ_EQUATION_FINITE_ELEMENT_CALCULATE::helmholtz_equation_finite_element_calculate(), hamilton_jacobi_equations_routines::HJ_EQUATION_FAST_MARCHING_CALCULATE::hj_equation_fast_marching_calculate(), hamilton_jacobi_equations_routines::HJ_EQUATION_FINITE_ELEMENT_CALCULATE::hj_equation_finite_element_calculate(), laplace_equations_routines::laplaceequation_finiteelementcalculate(), linear_elasticity_routines::linear_elasticity_finite_element_calculate(), monodomain_equations_routines::Monodomain_FiniteElementCalculate::monodomain_finiteelementcalculate(), navier_stokes_equations_routines::NavierStokes_CalculateElementMetrics::navierstokes_calculateelementmetrics(), navier_stokes_equations_routines::NavierStokes_FiniteElementJacobianEvaluate::navierstokes_finiteelementjacobianevaluate(), navier_stokes_equations_routines::NavierStokes_FiniteElementResidualEvaluate::navierstokes_finiteelementresidualevaluate(), navier_stokes_equations_routines::NavierStokes_ResidualBasedStabilisation::navierstokes_residualbasedstabilisation(), poisson_equations_routines::poisson_equation_finite_element_calculate(), poisson_equations_routines::poisson_finiteelementresidualevaluate(), reaction_diffusion_equation_routines::ReactionDiffusion_FiniteElementCalculate::reactiondiffusion_finiteelementcalculate(), and stokes_equations_routines::stokes_finite_element_calculate().
| integer(intg), dimension(20) constants::partial_derivative_global_derivative_map = [ NO_GLOBAL_DERIV,GLOBAL_DERIV_S1,0,GLOBAL_DERIV_S2,0, GLOBAL_DERIV_S1_S2,GLOBAL_DERIV_S3,0,GLOBAL_DERIV_S1_S3,GLOBAL_DERIV_S2_S3,GLOBAL_DERIV_S1_S2_S3,0,0,0,0,0,0,0,0,0 ] |
PARTIAL_DERIVATIVE_GLOBAL_DERIVATIVE_MAP(nu) gives the global derivative index for the the nu'th partial derivative. If no global derivative exists the map is zero.
Definition at line 262 of file constants.f90.
Partial derivative index map. PARTIAL_DERIVATIVE_INDEX(idx,nic) gives the order of the partial derivative in the ni(c)'th direction for the idx'th partial derivative value.
Definition at line 232 of file constants.f90.
Referenced by basis_routines::basis_lhtp_basis_evaluate_dp(), basis_routines::basis_simplex_basis_derivative_evaluate(), and field_io_routines::field_io_export_nodal_group_header_fortran().
| integer(intg), dimension(4) constants::partial_derivative_maximum_map = [ PART_DERIV_S1_S1,PART_DERIV_S1_S2,PART_DERIV_S1_S2_S3, PART_DERIV_S4_S4_S4 ] |
PARTIAL_DERIVATIVE_MAXIMUM_MAP(nic) gives the maximum of partial derivative index for the the ni(c)'th direction.
Definition at line 259 of file constants.f90.
| integer(intg), dimension(4) constants::partial_derivative_second_derivative_map = [ PART_DERIV_S1_S1,PART_DERIV_S2_S2,PART_DERIV_S3_S3, PART_DERIV_S4_S4 ] |
PARTIAL_DERIVATIVE_SECOND_DERIVATIVE_MAP(nic) gives the partial derivative index for the second derivative in the ni(c)'th direction.
Definition at line 256 of file constants.f90.
Referenced by coordinate_routines::coordinate_metrics_calculate(), and coordinate_routines::coordinate_system_normal_calculate().
| integer(intg), dimension(2,2), parameter constants::tensor_to_voigt2 =RESHAPE([1,3,3,2], [2,2]) |
Definition at line 284 of file constants.f90.
| integer(intg), dimension(3,3), parameter constants::tensor_to_voigt3 =RESHAPE([1,4,5,4,2,6,5,6,3], [3,3]) |
| integer(intg), dimension(2,3), parameter constants::voigt_to_tensor2 =RESHAPE([1,1,2,2,1,2], [2,3]) |
Definition at line 285 of file constants.f90.
| integer(intg), dimension(2,6), parameter constants::voigt_to_tensor3 =RESHAPE([1,1,2,2,3,3,1,2,1,3,2,3], [2,6]) |
Definition at line 287 of file constants.f90.
Referenced by finite_elasticity_routines::finite_elasticity_push_elasticity_tensor(), and finite_elasticity_routines::finite_elasticity_push_stress_tensor().
